LB formula for edge states

Some simple codes about Landauer-Buttiker formula.

1. Landauer-Buttiker Formula

Landauer-Buttiker formalism为$I_i = \frac{e^2}{h}\sum_{j\neq i } [T_{ji}V_i - T_{ij}V_j]$，无论系统的时间反演是否破缺，该公式都成立。

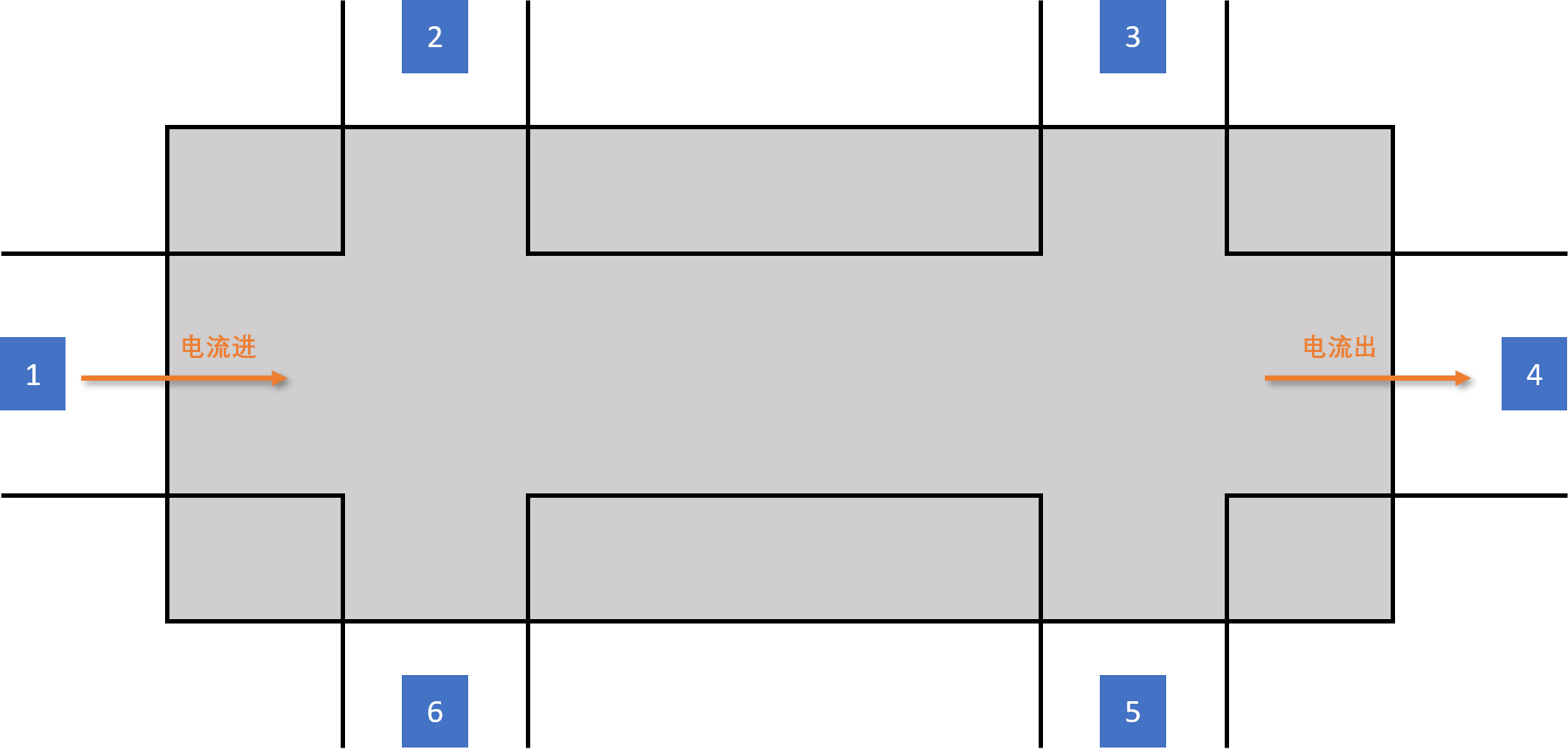
在这里，我们采用的是六电极的构型（如下图 所示），并且约定：电流端为1和4，电流1进4出，即$I_1 = - I_4 = I$，而其它电极(2,3,5,6)则作为电压端，不通电流，即$I_2 = I_3 = I_5 = I_6 = 0$，那么将Landauer-Buttiker公式写成矩阵的形式应为：

$$\begin{align} \left[ \begin{array}{c} I \\ 0 \\ 0 \\ -I \\ 0 \\ 0 \end{array} \right] & = \frac{e^2}{h} \left[ \begin{array}{cccccc} \sum_{i\neq 1}T_{i1} & -T_{12} & -T_{13} & -T_{14} & -T_{15} & -T_{16} \\ -T_{21} & \sum_{i\neq 2}T_{i2} & -T_{23} & -T_{24} & -T_{25} & -T_{26} \\ -T_{31} & -T_{32} & \sum_{i\neq 3}T_{i3} & -T_{34} & -T_{35} & -T_{36} \\ -T_{41} & -T_{42} & -T_{43} & \sum_{i\neq 4}T_{i4} & -T_{45} & -T_{46} \\ -T_{51} & -T_{52} & -T_{53} & -T_{54} & \sum_{i\neq 5}T_{i5} & -T_{56} \\ -T_{61} & -T_{62} & -T_{63} & -T_{64} & -T_{65} & \sum_{i\neq 6}T_{i6} \\ \end{array} \right] \left[ \begin{array}{c} V_{1} \\ V_{2} \\ V_{3} \\ V_{4} \\ V_{5} \\ V_{6} \end{array} \right] \end{align}$$

2. Quantum Hall Effect

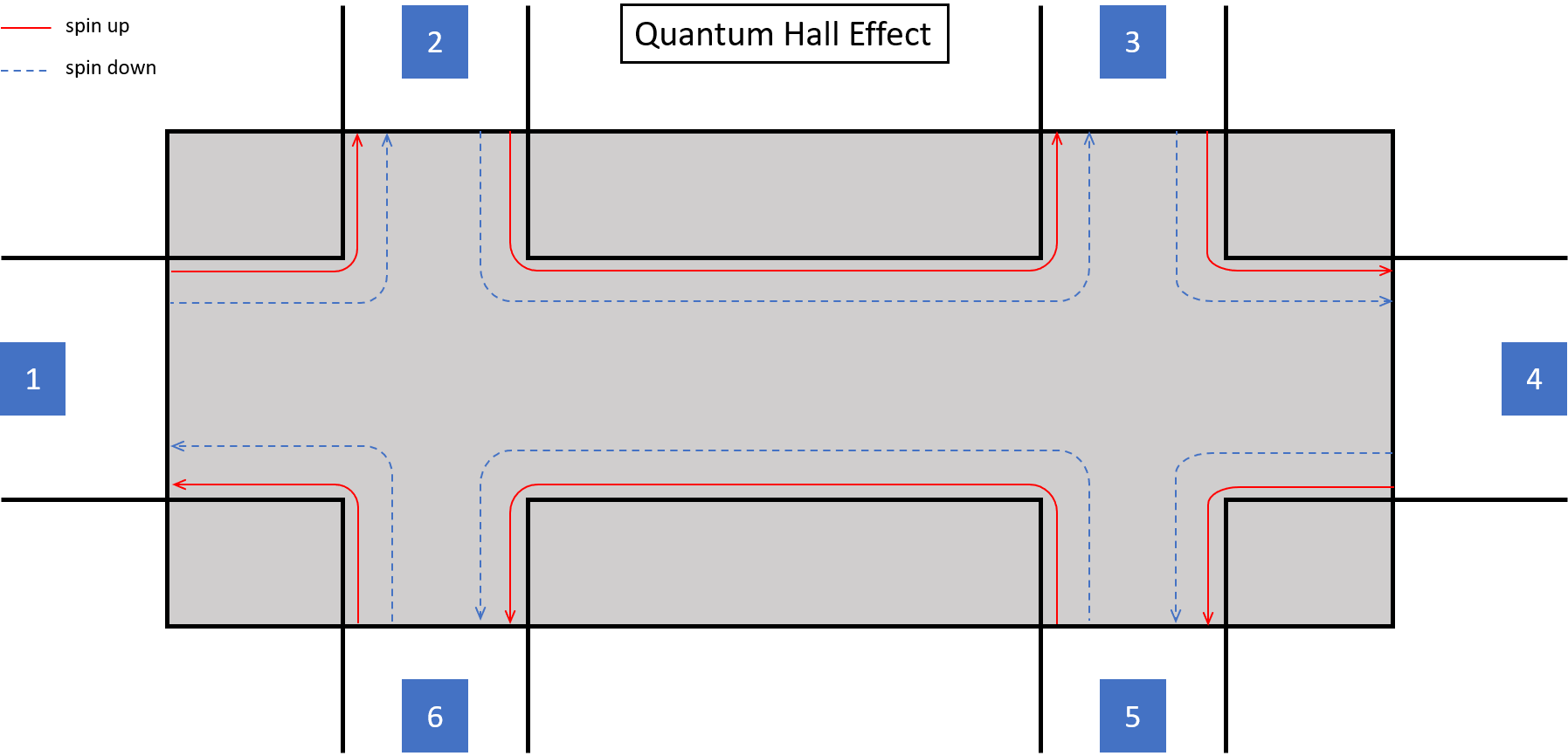
QHE的六电极构型如下图 所示，在这里我们考虑自旋向上和自旋向下两个通道。在QHE中，在边缘处所有边界态的运动方向都是一致的，这样的边界态也被称为chiral edge state。

在QHE的六电极构型中，只有相邻的两个电极之间有直接的电子传递，并且由于具有手性，6电极中的电子只能沿着两个通道（红色实线和蓝色虚线）运动到1电极，

同理，

1电极中的电子只能沿着两个通道（红色实线和蓝色虚线）运动到2电极，

2电极中的电子只能沿着两个通道（红色实线和蓝色虚线）运动到3电极，

3电极中的电子只能沿着两个通道（红色实线和蓝色虚线）运动到4电极，

4电极中的电子只能沿着两个通道（红色实线和蓝色虚线）运动到5电极，

5电极中的电子只能沿着两个通道（红色实线和蓝色虚线）运动到6电极，

因此其T矩阵的矩阵元为：

$$T_{16} = 2,T_{21} = 2,T_{32} = 2,T_{43} = 2, T_{54} = 2, T_{65} = 2,$$

其它矩阵元均为0，代入Landauer-Buttiker的矩阵公式中有

$$\begin{equation} \left[ \begin{array}{c} I \\ 0 \\ 0 \\ -I \\ 0 \\ 0 \end{array} \right] = \frac{e^2}{h} \left[ \begin{array}{cccccc} 2 & 0 & 0 & 0 & 0 & -2 \\ -2 & 2 & 0 & 0 & 0 & 0 \\ 0 & -2 & 2 & 0 & 0 & 0 \\ 0 & 0 & -2 & 2 & 0 & 0 \\ 0 & 0 & 0 & -2 & 2 & 0 \\ 0 & 0 & 0 & 0 & -2 & 2 \\ \end{array} \right] \left[ \begin{array}{c} V_{1} \\ V_{2} \\ V_{3} \\ V_{4} \\ V_{5} \\ V_{6} \end{array} \right] \end{equation}$$

通过高斯消元法，可以将这个方程组化简为：

$$\begin{equation} \left[ \begin{array}{c} 0.5I \\ 0.5I \\ 0.5I \\ 0 \\ 0 \\ 0 \end{array} \right] = \frac{e^2}{h} \left[ \begin{array}{cccccc} 1 & 0 & 0 & 0 & 0 & -1 \\ 0 & 1 & 0 & 0 & 0 & -1 \\ 0 & 0 & 1 & 0 & 0 & -1 \\ 0 & 0 & 0 & 1 & 0 & -1 \\ 0 & 0 & 0 & 0 & 1 & -1 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ \end{array} \right] \left[ \begin{array}{c} V_{1} \\ V_{2} \\ V_{3} \\ V_{4} \\ V_{5} \\ V_{6} \end{array} \right] \end{equation}$$

根据该方程组，可以很容易得到：

$$\frac{e^2}{h}(V_1 - V_4) = 0.5I, (V_2 - V_3) = 0, (V_6 - V_5) = 0, \frac{e^2}{h}(V_2-V_6) = 0.5I, \frac{e^2}{h}(V_3-V_5) = 0.5I$$

可以发现四端法纵向电阻为零，$R_{14,23} = R_{14,65} = 0$，但是在两端法下纵向电导并不为零，为2倍量子电导$G_{14,14}=2\frac{e^2}{h}$，而对于四端法横向电导则为两倍量子电导，$G_{14,26}=G_{14,35}=2\frac{e^2}{h}$。

LB code for QHE

n_terminal = 6;

% current probes
current_in = 1;
current_out = 4;
I = zeros(n_terminal, 1);
I(current_in) = 1;
I(current_out) = -1;

% 对于Quantum Hall Effect（两个通道）
T = zeros(n_terminal);
for i = 1:n_terminal
    T(i,i) = 2;
    
    next = rem(5+i, n_terminal);
    
    if next == 0
        T(i, next + n_terminal) = -2;
    else
        T(i, next) = -2;
    end
end


G = [T,I];

%% 做高斯消元法
% % 从第一行到最后一行
vec_temp = zeros(1, n_terminal+1);
for i = 1:(n_terminal-1)
    % 如果G(i,i) == 0则要交换一下行
    if G(i,i) == 0
        for ii = (i+1):n_terminal
            if ~(G(ii, i) == 0)
                vec_temp = G(ii, :);
                G(ii, :) = G(i, :);
                G(i, :) = vec_temp;
                break
            end
        end
    end
    
    % 如果G(i,i)仍然为0则直接跳过进行(i+1)
    if G(i, i) == 0
        continue
    end
    
    % 第i分量的高斯消元
    for j = (i+1):n_terminal
        if ~(G(j,i) == 0)
            ratio = G(j,i) / G(i,i);
            G(j,:) = G(j,:) - ratio * G(i,:);
        end
    end
end

% % 从最后一行到第一行
for i = n_terminal:-1:2
    % 如果G(i,i) == 0则跳过直接下一步
    if abs(G(i,i)) < 1e-8
        continue
    end
    
    % 先对第i行进行归一化
    G(i, :) = G(i, :) / G(i, i);
    
    % 第i分量的高斯消元
    for j = (i-1):-1:1
        if ~(G(j,i) == 0)
            ratio = G(j,i);
            G(j,:) = G(j,:) - ratio * G(i,:);
        end
    end
end
% 最后对第1行进行归一化
G(1, :) = G(1, :) / G(1, 1);


%% 计算电导
% 计算two-terminal 或 four-terminal conductance
% % voltage probes
v_left = 2;
v_right = 3;

ratio = G(v_right, end-1) / G(v_left, end-1);
if abs(abs(ratio)-1) > 1e-8
    disp("some problems")
end

delta_G = G(v_right, end) - G(v_left, end);

3. Quantum Spin Hall Effect

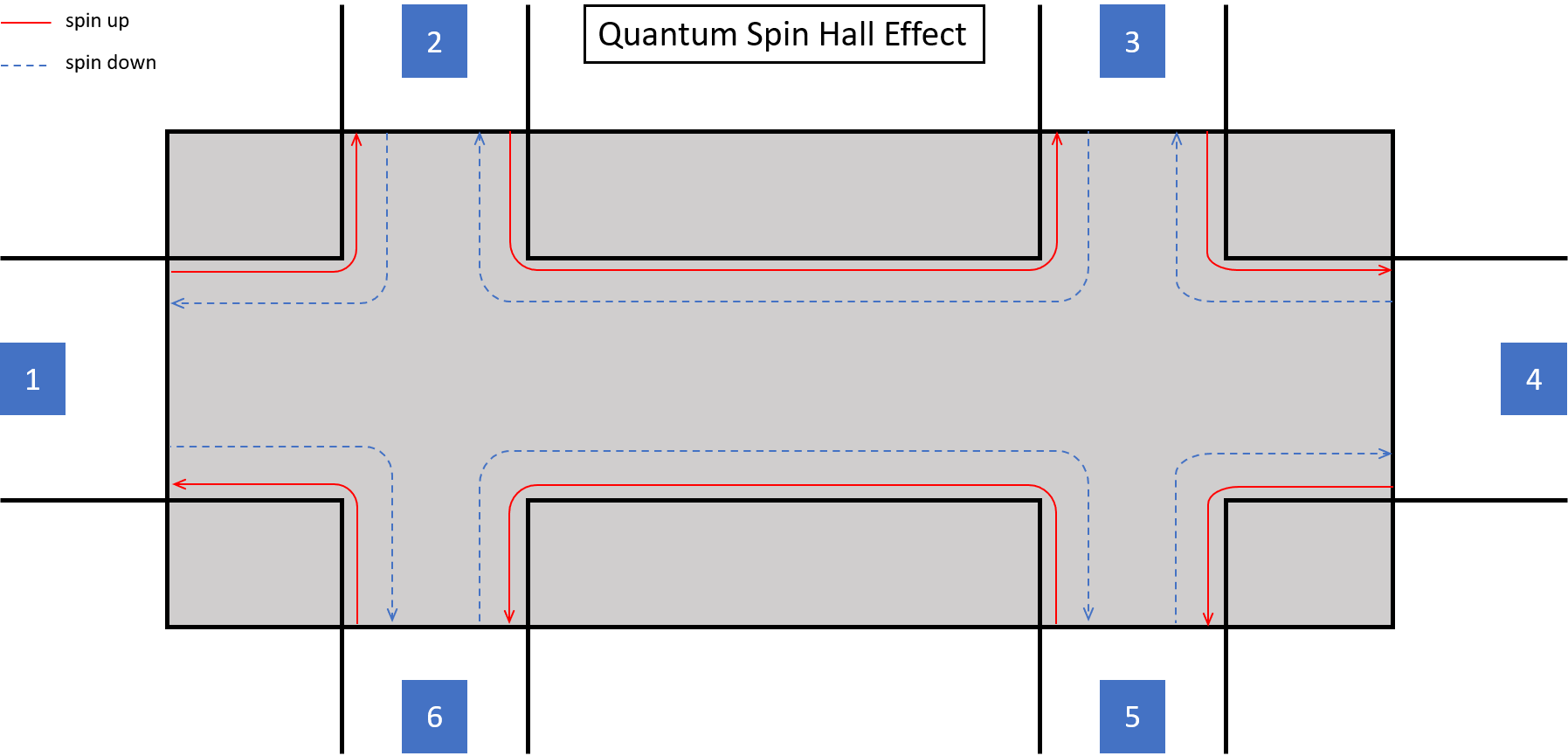
QSHE的六电极构型如下图 所示，在这里我们考虑自旋向上和自旋向下两个通道。在QSHE中，在边缘处自旋向上与自旋向下的边界态的运动方向是相反的，这体现了系统的时间反演对称性，而这样的边界态也被称为helical edge state。

在QSHE的六电极构型中，只有相邻的两个电极之间有直接的电子传递，并且由于是helical edge state，

6电极中的电子可以沿着一个通道（红色实线）边缘运动到1电极，而沿着另一个通道（蓝色虚线）边缘运动到5电极，

同理，

1电极中的电子可以沿着一个通道（红色实线）边缘运动到2电极，而沿着另一个通道（蓝色虚线）边缘运动到6电极，

2电极中的电子可以沿着一个通道（红色实线）边缘运动到3电极，而沿着另一个通道（蓝色虚线）边缘运动到1电极，

3电极中的电子可以沿着一个通道（红色实线）边缘运动到4电极，而沿着另一个通道（蓝色虚线）边缘运动到2电极，

4电极中的电子可以沿着一个通道（红色实线）边缘运动到5电极，而沿着另一个通道（蓝色虚线）边缘运动到3电极，

5电极中的电子可以沿着一个通道（红色实线）边缘运动到6电极，而沿着另一个通道（蓝色虚线）边缘运动到4电极，

因此其T矩阵的矩阵元为：

$$T_{61} = T_{16} = 1, T_{21} = T_{12} = 1, T_{32} = T_{23} = 1, T_{43} = T_{34} = 1, T_{45} = T_{54} = 1, T_{56} = T_{65} = 1$$

其它矩阵元均为0，代入Landauer-Buttiker的矩阵公式中有：

$$\begin{equation} \left[ \begin{array}{c} I \\ 0 \\ 0 \\ -I \\ 0 \\ 0 \end{array} \right] = \frac{e^2}{h} \left[ \begin{array}{cccccc} 2 & -1 & 0 & 0 & 0 & -1 \\ -1 & 2 & -1 & 0 & 0 & 0 \\ 0 & -1 & 2 & -1 & 0 & 0 \\ 0 & 0 & -1 & 2 & -1 & 0 \\ 0 & 0 & 0 & -1 & 2 & -1 \\ -1 & 0 & 0 & 0 & -1 & 2 \\ \end{array} \right] \left[ \begin{array}{c} V_{1} \\ V_{2} \\ V_{3} \\ V_{4} \\ V_{5} \\ V_{6} \end{array} \right] \end{equation}$$

通过高斯消元法，可以将这个方程组化简为：

$$\begin{equation} \left[ \begin{array}{c} 0.5I \\ 0 \\ -0.5I \\ -I \\ -0.5I \\ 0 \end{array} \right] = \frac{e^2}{h} \left[ \begin{array}{cccccc} 1 & 0 & 0 & 0 & 0 & -1 \\ 0 & 1 & 0 & 0 & 0 & -1 \\ 0 & 0 & 1 & 0 & 0 & -1 \\ 0 & 0 & 0 & 1 & 0 & -1 \\ 0 & 0 & 0 & 0 & 1 & -1 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ \end{array} \right] \left[ \begin{array}{c} V_{1} \\ V_{2} \\ V_{3} \\ V_{4} \\ V_{5} \\ V_{6} \end{array} \right] \end{equation}$$

根据该方程组，可以很容易得到：

$$\frac{e^2}{h}(V_1 - V_4) = 1.5I, \frac{e^2}{h}(V_2 - V_3) = 0.5I, \frac{e^2}{h}(V_6 - V_5) = 0.5I, (V_2-V_6) = 0, (V_3-V_5) = 0$$

可以发现四端法纵向电导为两倍量子电导，$G_{14, 23} = G_{14, 65}= 2\frac{e^2}{h}$

两端法纵向电导为$\frac{2}{3}$倍量子电导 $G_{14, 14} = \frac{2}{3}\frac{e^2}{h}$

而对于四端法横向电阻则都为零，$R_{14, 26} = R_{14, 35} = 0$

LB code for QSHE

n_terminal = 6;

% current probes
current_in = 1;
current_out = 4;
I = zeros(n_terminal, 1);
I(current_in) = 1;
I(current_out) = -1;

% 对于Quantum Spin Hall Effect
T = zeros(n_terminal);
for i = 1:n_terminal
    T(i,i) = 2;
    
    left = rem(i-1, n_terminal);
    right = rem(i+1, n_terminal);
    
    if left == 0
        T(i, left + n_terminal) = -1;
    else
        T(i, left) = -1;
    end
    
    if right == 0
        T(i, right + n_terminal) = -1;
    else
        T(i, right) = -1;
    end
end

G = [T,I];

%% 做高斯消元法
% % 从第一行到最后一行
vec_temp = zeros(1, n_terminal+1);
for i = 1:(n_terminal-1)
    % 如果G(i,i) == 0则要交换一下行
    if G(i,i) == 0
        for ii = (i+1):n_terminal
            if ~(G(ii, i) == 0)
                vec_temp = G(ii, :);
                G(ii, :) = G(i, :);
                G(i, :) = vec_temp;
                break
            end
        end
    end
    
    % 如果G(i,i)仍然为0则直接跳过进行(i+1)
    if G(i, i) == 0
        continue
    end
    
    % 第i分量的高斯消元
    for j = (i+1):n_terminal
        if ~(G(j,i) == 0)
            ratio = G(j,i) / G(i,i);
            G(j,:) = G(j,:) - ratio * G(i,:);
        end
    end
end

% % 从最后一行到第一行
for i = n_terminal:-1:2
    % 如果G(i,i) == 0则跳过直接下一步
    if abs(G(i,i)) < 1e-8
        continue
    end
    
    % 先对第i行进行归一化
    G(i, :) = G(i, :) / G(i, i);
    
    % 第i分量的高斯消元
    for j = (i-1):-1:1
        if ~(G(j,i) == 0)
            ratio = G(j,i);
            G(j,:) = G(j,:) - ratio * G(i,:);
        end
    end
end
% 最后对第1行进行归一化
G(1, :) = G(1, :) / G(1, 1);


%% 计算电导
% 计算two-terminal 或 four-terminal conductance
% % voltage probes
v_left = 2;
v_right = 3;

ratio = G(v_right, end-1) / G(v_left, end-1);
if abs(abs(ratio)-1) > 1e-8
    disp("some problems")
end

delta_G = G(v_right, end) - G(v_left, end);

4. Quantum Parity Hall Effect

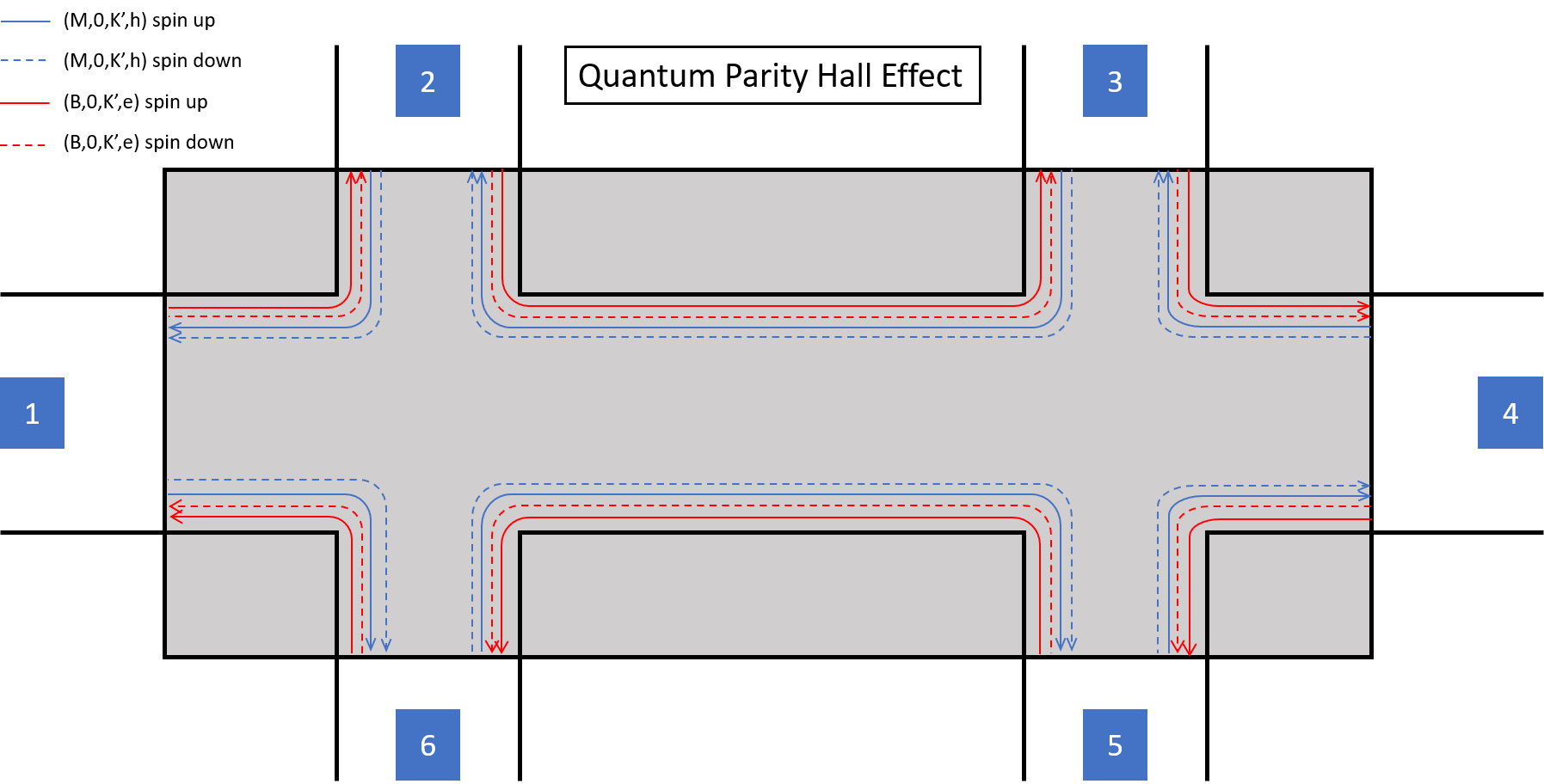
QPHE的六电极构型如下图 所示，在这里需要考虑四个通道，其中两个是来自自旋简并的单层石墨烯中空穴型朗道能级，

另外两个则是来自自旋简并的双层石墨烯中电子型朗道能级。

在QPHE中，在边缘处来自单层与来自双层的边界态的运动方向是相反的，这是因为一个是空穴型另一个是电子型的缘故，但每个朗道能级中自旋向上和

自旋向下的边界态的运动方向是一致的，这样的边界态也被称为helical edge state，但是与QSHE不同，这里是单层与双层的边界态运动方向不同

而不是自旋相反的边界态运动方向不同，它破坏了时间反演对称性，但是受到了镜面对称性的保护。

在QPHE的六电极构型中，只有相邻的两个电极之间有直接的电子传递，并且由于是helical edge state，

6电极中的电子可以沿着两个通道（红色实线和红色虚线）边缘运动到1电极，而沿着另两个通道（蓝色实线和蓝色虚线）边缘运动到5电极，

同理，

1电极中的电子可以沿着两个通道（红色实线和红色虚线）边缘运动到2电极，而沿着另两个通道（蓝色实线和蓝色虚线）边缘运动到6电极，

2电极中的电子可以沿着两个通道（红色实线和红色虚线）边缘运动到3电极，而沿着另两个通道（蓝色实线和蓝色虚线）边缘运动到1电极，

3电极中的电子可以沿着两个通道（红色实线和红色虚线）边缘运动到4电极，而沿着另两个通道（蓝色实线和蓝色虚线）边缘运动到2电极，

4电极中的电子可以沿着两个通道（红色实线和红色虚线）边缘运动到5电极，而沿着另两个通道（蓝色实线和蓝色虚线）边缘运动到3电极，

5电极中的电子可以沿着两个通道（红色实线和红色虚线）边缘运动到6电极，而沿着另两个通道（蓝色实线和蓝色虚线）边缘运动到4电极，

因此其T矩阵的矩阵元为：

$$T_{61} = T_{16} = 2, T_{21} = T_{12} = 2, T_{32} = T_{23} = 2, T_{43} = T_{34} = 2, T_{45} = T_{54} = 2, T_{56} = T_{65} = 2$$

其它矩阵元均为0，代入Landauer-Buttiker的矩阵公式中有：

$$\begin{equation} \left[ \begin{array}{c} I \\ 0 \\ 0 \\ -I \\ 0 \\ 0 \end{array} \right] = \frac{e^2}{h} \left[ \begin{array}{cccccc} 4 & -2 & 0 & 0 & 0 & -2 \\ -2 & 4 & -2 & 0 & 0 & 0 \\ 0 & -2 & 4 & -2 & 0 & 0 \\ 0 & 0 & -2 & 4 & -2 & 0 \\ 0 & 0 & 0 & -2 & 4 & -2 \\ -2 & 0 & 0 & 0 & -2 & 4 \\ \end{array} \right] \left[ \begin{array}{c} V_{1} \\ V_{2} \\ V_{3} \\ V_{4} \\ V_{5} \\ V_{6} \end{array} \right] \end{equation}$$

通过高斯消元法，可以将这个方程组化简为：

$$\begin{equation} \left[ \begin{array}{c} 0.25I \\ 0 \\ -0.25I \\ -0.5I \\ -0.25I \\ 0 \end{array} \right] = \frac{e^2}{h} \left[ \begin{array}{cccccc} 1 & 0 & 0 & 0 & 0 & -1 \\ 0 & 1 & 0 & 0 & 0 & -1 \\ 0 & 0 & 1 & 0 & 0 & -1 \\ 0 & 0 & 0 & 1 & 0 & -1 \\ 0 & 0 & 0 & 0 & 1 & -1 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ \end{array} \right] \left[ \begin{array}{c} V_{1} \\ V_{2} \\ V_{3} \\ V_{4} \\ V_{5} \\ V_{6} \end{array} \right] \end{equation}$$

根据该方程组，可以很容易得到：

$$\frac{e^2}{h}(V_1 - V_4) = 0.75I, \frac{e^2}{h}(V_2 - V_3) = 0.25I, \frac{e^2}{h}(V_6 - V_5) = 0.25I, (V_2-V_6) = 0, (V_3-V_5) = 0$$

可以发现四端法纵向电导为四倍量子电导，$G_{14, 23} = G_{14, 65}= 4\frac{e^2}{h}$

两端法纵向电导为$\frac{4}{3}$倍量子电导 $G_{14, 14} = \frac{4}{3}\frac{e^2}{h}$

而对于四端法横向电阻则都为零，$R_{14, 26} = R_{14, 35} = 0$

LB code for QPHE

n_terminal = 6;

% current probes
current_in = 1;
current_out = 4;
I = zeros(n_terminal, 1);
I(current_in) = 1;
I(current_out) = -1;

% 对于Quantum Parity Hall Effect
T = zeros(n_terminal);
for i = 1:n_terminal
    T(i,i) = 4;
    
    left = rem(i-1, n_terminal);
    right = rem(i+1, n_terminal);
    
    if left == 0
        T(i, left + n_terminal) = -2;
    else
        T(i, left) = -2;
    end
    
    if right == 0
        T(i, right + n_terminal) = -2;
    else
        T(i, right) = -2;
    end
end

G = [T,I];

%% 做高斯消元法
% % 从第一行到最后一行
vec_temp = zeros(1, n_terminal+1);
for i = 1:(n_terminal-1)
    % 如果G(i,i) == 0则要交换一下行
    if G(i,i) == 0
        for ii = (i+1):n_terminal
            if ~(G(ii, i) == 0)
                vec_temp = G(ii, :);
                G(ii, :) = G(i, :);
                G(i, :) = vec_temp;
                break
            end
        end
    end
    
    % 如果G(i,i)仍然为0则直接跳过进行(i+1)
    if G(i, i) == 0
        continue
    end
    
    % 第i分量的高斯消元
    for j = (i+1):n_terminal
        if ~(G(j,i) == 0)
            ratio = G(j,i) / G(i,i);
            G(j,:) = G(j,:) - ratio * G(i,:);
        end
    end
end

% % 从最后一行到第一行
for i = n_terminal:-1:2
    % 如果G(i,i) == 0则跳过直接下一步
    if abs(G(i,i)) < 1e-8
        continue
    end
    
    % 先对第i行进行归一化
    G(i, :) = G(i, :) / G(i, i);
    
    % 第i分量的高斯消元
    for j = (i-1):-1:1
        if ~(G(j,i) == 0)
            ratio = G(j,i);
            G(j,:) = G(j,:) - ratio * G(i,:);
        end
    end
end
% 最后对第1行进行归一化
G(1, :) = G(1, :) / G(1, 1);


%% 计算电导
% 计算two-terminal 或 four-terminal conductance
% % voltage probes
v_left = 2;
v_right = 3;

ratio = G(v_right, end-1) / G(v_left, end-1);
if abs(abs(ratio)-1) > 1e-8
    disp("some problems")
end

delta_G = G(v_right, end) - G(v_left, end);