simple codes on finite element method

Some simple codes on finite element method, including both 1D and 2D case.

有限元模拟的基本步骤包括：

  • 建立几何模型
  • 网格划分
  • 得到有限元矩阵并求解
  • 后处理

其中建立几何模型和网格划分往往需要借助CAD，这里介绍的只是对于一些简单的问题如何得到有限元矩阵并求解之。当然，做有限元模拟的大前提是知道物理场的方程是什么以及边界条件是什么。

  1. some basic elements

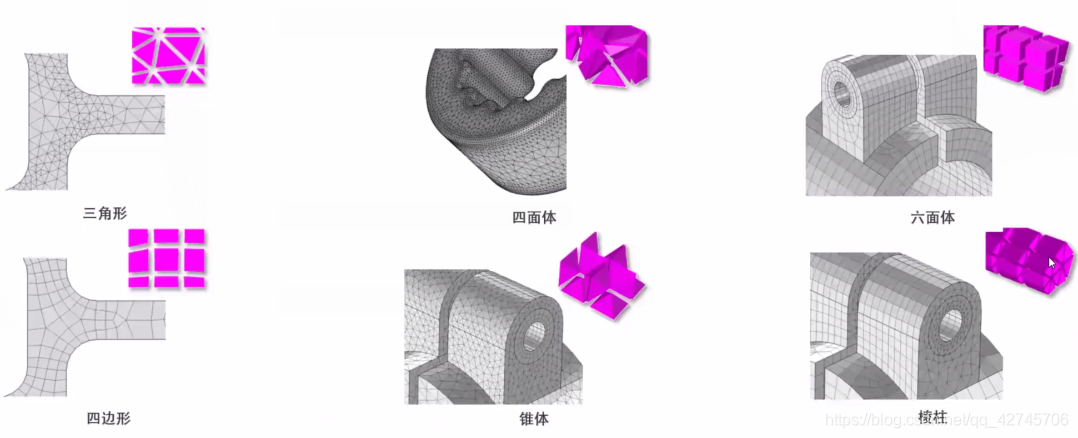
    • 网格划分

    做有限元的第一步通常是网格划分，网格划分有各种类型。


    • 形函数

    划分完网格之后，要求的就是这些离散格点上的函数值（或者说是物理场的值）。

    但是物理场本身是一个连续的量，这就需要用到形函数来构建两者之间的桥梁，将那些非格点的区域的函数形貌用紧邻的格点函数值来描述，当格点越密，这种方式显然是越精确。


    一维情形，一阶形函数有两个， NL(r)=12(1−r),NR(r)=12(1+r)N_L(r) = \frac{1}{2}(1 - r), N_R(r) = \frac{1}{2}(1 + r)

    二维情形，在标准单位上的二维形函数有四个，分别为

    N1(r,s)=14(1−r)(1−s)N2(r,s)=14(1+r)(1−s)N3(r,s)=14(1+r)(1+s)N4(r,s)=14(1−r)(1+s)\small{ \begin{align} N_1(r, s) = \frac{1}{4}(1 - r)(1 - s) & &\\ N_2(r, s) = \frac{1}{4}(1 + r)(1 - s) & &\\ N_3(r, s) = \frac{1}{4}(1 + r)(1 + s) & &\\ N_4(r, s) = \frac{1}{4}(1 - r)(1 + s) & &\\ \end{align} }

    以及相应的偏导数为 ：

    ∂∂rN1(r,s)=−14(1−s)∂∂sN1(r,s)=−14(1−r)∂∂rN2(r,s)=+14(1−s)∂∂sN2(r,s)=−14(1+r)∂∂rN3(r,s)=+14(1+s)∂∂sN3(r,s)=+14(1+r)∂∂rN4(r,s)=−14(1+s)∂∂sN4(r,s)=+14(1−r)\small{ \begin{align} \frac{\partial}{\partial r} N_1(r, s) = - \frac{1}{4}(1 - s) & & \frac{\partial}{\partial s} N_1(r, s) = - \frac{1}{4}(1 - r) & &\\ \frac{\partial}{\partial r} N_2(r, s) = + \frac{1}{4}(1 - s) & & \frac{\partial}{\partial s} N_2(r, s) = - \frac{1}{4}(1 + r) & &\\ \frac{\partial}{\partial r} N_3(r, s) = + \frac{1}{4}(1 + s) & & \frac{\partial}{\partial s} N_3(r, s) = + \frac{1}{4}(1 + r) & &\\ \frac{\partial}{\partial r} N_4(r, s) = - \frac{1}{4}(1 + s) & & \frac{\partial}{\partial s} N_4(r, s) = + \frac{1}{4}(1 - r) & &\\ \end{align} }

    习惯上会将它们整合成一个矩阵的形式：

    std_shape_partial_mat=[∂∂rN1(r,s)∂∂rN2(r,s)∂∂rN3(r,s)∂∂rN4(r,s)∂∂sN1(r,s)∂∂sN2(r,s)∂∂sN3(r,s)∂∂sN4(r,s)]\text{std\_shape\_partial\_mat} = \begin{bmatrix} \frac{\partial}{\partial r} N_1(r, s) & \frac{\partial}{\partial r} N_2(r, s) & \frac{\partial}{\partial r} N_3(r, s) & \frac{\partial}{\partial r} N_4(r, s) \\ \\ \frac{\partial}{\partial s} N_1(r, s) & \frac{\partial}{\partial s} N_2(r, s) & \frac{\partial}{\partial s} N_3(r, s) & \frac{\partial}{\partial s} N_4(r, s) \\ \end{bmatrix}

    • 雅可比矩阵

    在做积分的时候，往往将积分区域通过坐标变换转换为标准区域上的积分，这个变换涉及雅可比矩阵

    一维情形的雅可比矩阵为1×11\times 1矩阵，J=∂x∂rJ = \frac{\partial x}{\partial r}；

    二维情形的雅可比矩阵为2×22\times 2矩阵，J=∂(x,y)∂(r,s)J = \frac{\partial (x, y)}{\partial (r, s)},

    对于一个任意的四边形（顶角坐标设为(xi,yi)(x_i, y_i)），其与标准单位四边形之间的雅可比变换矩阵形式为：

    Jmat=∂(x,y)∂(r,s)=[∂x∂r∂y∂r∂x∂s∂y∂s]=[∑j∂Nj(r,s)∂rxj∑j∂Nj(r,s)∂ryj∑j∂Nj(r,s)∂sxj∑j∂Nj(r,s)∂syj]=[∂N1(r,s)∂r∂N2(r,s)∂r∂N3(r,s)∂r∂N4(r,s)∂r∂N1(r,s)∂s∂N2(r,s)∂s∂N3(r,s)∂s∂N4(r,s)∂s][x1y1x2y2x3y3x4y4]=std_shape_partial_mat⊗[x1y1x2y2x3y3x4y4]J_{mat} = \frac{\partial (x, y)}{\partial (r, s)} = \begin{bmatrix} \frac{\partial x}{\partial r} & \frac{\partial y}{\partial r} \\ \frac{\partial x}{\partial s} & \frac{\partial y}{\partial s} \end{bmatrix} = \begin{bmatrix} \sum_j \frac{\partial N_j(r,s)}{\partial r}x_j & \sum_j \frac{\partial N_j(r,s)}{\partial r}y_j\\ \sum_j \frac{\partial N_j(r,s)}{\partial s}x_j & \sum_j \frac{\partial N_j(r,s)}{\partial s}y_j \end{bmatrix} \\ = \begin{bmatrix} \frac{\partial N_1(r,s)}{\partial r} & \frac{\partial N_2(r,s)}{\partial r} & \frac{\partial N_3(r,s)}{\partial r} & \frac{\partial N_4(r,s)}{\partial r} \\ \frac{\partial N_1(r,s)}{\partial s} & \frac{\partial N_2(r,s)}{\partial s} & \frac{\partial N_3(r,s)}{\partial s} & \frac{\partial N_4(r,s)}{\partial s} \\ \end{bmatrix} \begin{bmatrix} x_1 & y_1 \\ x_2 & y_2 \\ x_3 & y_3 \\ x_4 & y_4 \end{bmatrix} \\ = \text{std\_shape\_partial\_mat} \otimes \begin{bmatrix} x_1 & y_1 \\ x_2 & y_2 \\ x_3 & y_3 \\ x_4 & y_4 \end{bmatrix}

    • 速度快且精度高的积分

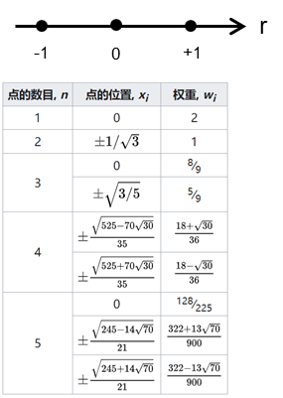
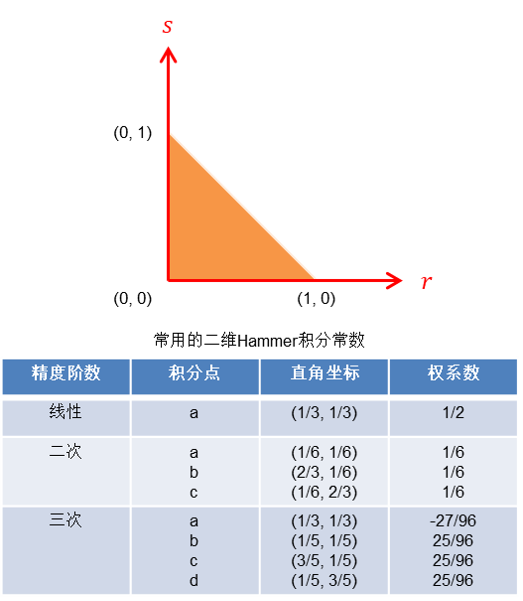
    由于通常使用多项式积分，这时候使用高斯求积公式（或Hammer求积公式）会大大提高计算效率，一般情况下用到前几阶的就已经完全严格了。


  2. a simple 1D case

    ∂2u∂x2=2u(1)=u(−1)=1\frac{\partial^2 u}{\partial x^2} = 2 \\ u(1) = u(-1) = 1

    It’s very easy to get the answer, so we can use it as a benchmark.

  3. a simple 2D case

    △u(x,y)=4,where −1≤x,y≤1with boundary condition : u(±1,y)=y2+1,u(x,±1)=x2+1\begin{align} \bigtriangleup u(x,y) = 4, & \text{where } -1 \le x,y \le 1 \\ \text{with boundary condition : }& u(\pm 1,y) = y^2 + 1, u(x,\pm 1) = x^2 + 1 \end{align}

Numerical Methods
#FEM
simple codes on finite element method
http://example.com/2023/04/26/FEM_simple/
Author
Shijie Fang
Posted on
April 26, 2023
Licensed under